Üç Kapı Problemi (Monty Hall)

Arkanıza yaslanın ve kendinizi bir yarışma programında hayal edin. Tribünde seyirciler, tepenizde göz kamaştıran spot lambaları ve yanınızda da gevşek bir yarışma sunucusu…

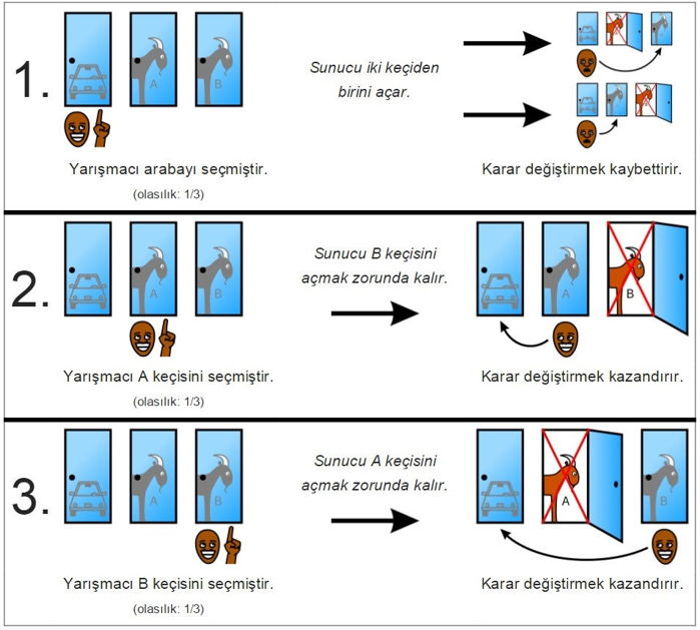
Sunucu, karşınızda duran perdeyi kaldırıyor ve perdenin arkasından 3 kapı ortaya çıkıyor. Size kapılardan birinin arkasında lüks bir arabanın ve diğer iki kapının ardında da keçi olduğundan bahsediliyor. Sonrasında yarışma sunucusu sizden bir kapı seçmenizi istiyor ve siz 3 kapıdan birini seçiyorsunuz.

Buraya kadar bir sorun yok sanırım. Devam ediyorum…

Sunucu, sizin seçtiğiniz kapıyı yüksek sesle seyircilere duyurduktan sonra size bir iyilik yapacağından bahsediyor ve diğer iki kapıdan arkasında keçi olan bir kapıyı açıyor. Geriye kalıyor iki kapı; biri sizin seçtiğiniz ve biri sunucunun size bıraktığı.

Sunucu size tekrar bir soru soruyor; seçtiğiniz kapıda kalıyor musunuz? Ya da seçiminizi değiştirmek ister misiniz?

Bu soru üzerine sizin tercihiniz ne olurdu?

Aslında sizin içine düştüğünüz durum, “Monty Hall Problemi” olarak bilinen ve ismini Amerikan TV yarışma programı Let’s Make a Deal’ın sunucusu Monty Hall’dan alan bir olasılık bulmacasıdır. İçinde bir paradoksu da barındırması nedeniyle Monty Hall Paradoksu olarak da anılan problemin sonucu saçma gibi görünse de ispatlanabilir ve doğrudur.

Genelde bu tür bir durumun içinde kalanlar, kapıların eşit olasılığa sahip olduğunu ve seçimi değiştirmenin hiçbir şeyi değiştirmeyeceğini düşünürler. Ama matematik bu durumu böyle düşünmez…

Matematik, size son durumda seçiminizi değiştirmenizi tavsiye eder. Çünkü böylece arabayı bulma olasılığınızı 1/3’ten 2/3’e çıkartmış olursunuz.

Monty Hall Problemi’ni Matematik Nasıl Görüyor?

Kapılardan birini seçtiğinizde, seçilen kapının ardında araba olma olasılığı 1/3’tür. Araba, 2/3 olasılıkla diğer kapılardan birinin ardındadır.

Sonra sunucu ardında keçi olan kapılardan birini açar ve geriye iki kapı kalır; biri sizin seçtiğiniz, diğeri de sunucunun size bıraktığı. Bu durumda elinizde ne olduğuna bakarsanız;

Sunucunun ardında keçi olan bir kapıyı açması, sizin seçtiğiniz kapının ardında ne olduğuyla ilgili yeni bir bilgi vermez. Sizin seçtiğiniz kapının ardında araba olma olasılığı hâlâ 1/3’tür. Açılan kapının ardında araba olma olasılığı ise 0/3 olur. Dolayısıyla araba 2/3 olasılıkla hâlâ açılmayan kapının ardındadır. Eğer kapı seçiminizi değiştirirseniz arabayı kazanma olasılığınız 2/3’e çıkacaktır.

Sonuç olarak; matematiğe göre arabayı kazanma şansınızı artırmak için seçiminizi değiştirmelisiniz.

Dipnot: “21” filminde MIT’de profesör olan Micky Rosa, öğrencisi Ben’e bu soruyu “konuk yarışmacı problemi” olarak soruyordu. Hocanın öğrencisinden aldığı cevap, benim yukarıda size anlattığımla aynı doğrultuda.

Bu ve buna benzer yazıları “5N1Kenar” kategorisinde yazacağım. Takipte kalın…

Allah (C.C.), çarşınıza pazar versin. Selametle…
Kaynak: Vikipedi